TABUNG

Pengertian Tabung

Tabung adalah bangun ruang yang dibatasi oleh dua bidang lingkaran yang sama besar dan sebangun (kongruen) yang berhadapan, sejajar, dan tiap titik yang bersesuaian pada kedua lingkaran tersebut saling dihubungkan dengan garis lurus.

Unsur-unsur Tabung

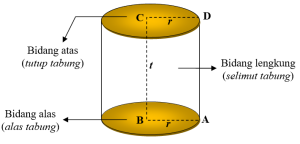
Keterangan:

r = AB = CD = jari-jari lingkaran

t = BC = tinggi tabung

Rumus-rumus Tabung

Rumus Luas Alas dan Tutup Tabung

Luas Alas   =  Luas lingkaran  =  πr²

Luas Tutup  =  Luas lingkaran  =  πr²

Rumus Luas Selimut Tabung

Luas Selimut  =  2 x π x r x t  =  2πrt

Rumus Luas Permukaan Tabung

Luas Permukaan Tabung  =  2 x π x r x (r + t)  =  2πr(r + t)

Rumus Volume Tabung

Volume Tabung  =  π x r x r x t  =  πr²t

KERUCUT

Pengertian Kerucut

Kerucut adalah bangun yang dibatasi oleh garis pelukis yang ujung-ujungnya bergerak mengelilingi sisi alas berupa lingkaran dan pangkalnya diam di titik puncak kerucut.

Unsur-unsur Kerucut

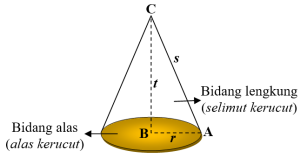
Keterangan:

t  =  tinggi kerucut (BC)

r  =  jari-jari (AB)

s  =  garis pelukis, yaitu garis yang menghubungkan titik puncak kerucut dengan titik pada keliling sisi alas kerucut (AC)

Sehingga berlaku Teorema Pythagoras:

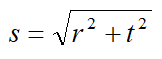
Rumus-rumus Kerucut

Rumus Luas Alas Kerucut

Luas Alas  =  Luas lingkaran  =  πr²

Rumus Luas Selimut Kerucut

Luas Selimut  =  π x r x s  =  πrs

Rumus Luas Permukaan Kerucut

Luas Permukaan  =  π x r x (r + s)  =  πr(r + s)

Rumus Volume Kerucut

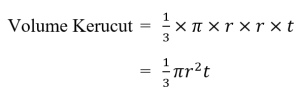
BOLA

Pengertian Bola

Bola adalah bangun ruang yang dibatasi oleh tempat kedudukan titik-titik yang berjarak sama (jari-jari) dari suatu titik tertentu (titik pusat)

Unsur-unsur Bola

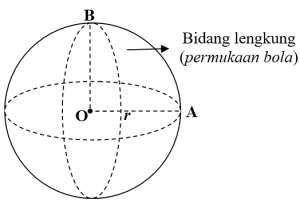
Keterangan:

r = AO = BO = jari-jari

O = titik pusat

Rumus-rumus Bola

Rumus Luas Permukaan Bola

Luas Permukaan Bola  =  4 x π x r x r  =  4πr²

Rumus Volume Bola

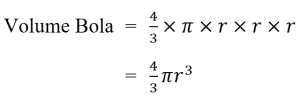
Rumus Luas Belahan Bola Padat

Luas Belahan Bola Padat  =  3 x π x r x r  =  3πr²

#SEMOGA BERMANFAAT#