Pola Barisan Konfigurasi Objek
Barisan bilangan merupakan susunan bilangan yang memiliki pola dan teratur.
Contoh :
Batang-batang korek api disusun seperti berikut.

Banyak batang korek api yang diperlukan adalah 4, 7, 10.
Banyak batang korek api yang diperlukan untuk pola selanjutnya yaitu dengan menambahkan sebanyak 3 batang korek api dari pola sebelumnya.
Jadi, susunan yang terjadi dari banyaknya batang korek api di atas memiliki pola dan teratur.
![]()
Pengertian Barisan Bilangan
Bilangan-bilangan yang disusun berdasarkan urutan dan pola tertentu akan membentuk suatu barisan bilangan. Bilangan-bilangan pada barisan bilangan tersebut dinamakan sebagai suku. Suku ke-n suatu barisan bilangan ditulis dengan (Un).
Contoh :
Perhatikan beberapa contoh barisan bilangan berikut.
- 1, 3, 5, 7
- 3, 6, 12, 24
- 1, 8, 27, 64
Jika kalian perhatikan, bilangan-bilangan tersebut di atas disusun dengan pola tertentu.
Pada barisan bilangan 1, 3, 5, 7 didapat:
Suku ke-1 = U1 = 1
Suku ke-2 = U2 = 3
Suku ke-3 = U3 = 5
Suku ke-4 = U4 = 7
Jadi, barisan bilangan 1, 3, 5, 7 memiliki 4 suku.
![]()
Barisan Bilangan Khusus dan Polanya
Barisan Bilangan Asli
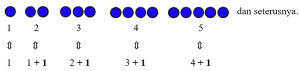
Barisan bilangan asli adalah 1, 2, 3, 4, 5, … .
Bilangan berikutnya diperoleh dengan cara menambahkan 1 pada bilangan sebelumnya.
Contoh :
![]()
Barisan Bilangan Ganjil
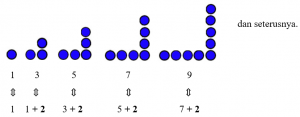
Barisan bilangan ganjil adalah 1, 3, 5, 7, 9, 11, … .
Bilangan berikutnya diperoleh dengan cara menambahkan 2 pada bilangan sebelumnya.
Contoh :
![]()
Barisan Bilangan Genap
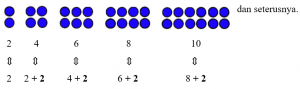
Barisan bilangan ganjil adalah 2, 4, 6, 8, 10, 12, … .
Bilangan berikutnya diperoleh dengan cara menambahkan 2 pada bilangan sebelumnya.
Contoh :
![]()
Barisan Bilangan Segitiga
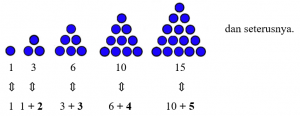
Barisan bilangan segitiga adalah 1, 3, 6, 10, 15, … .
Contoh :
![]()
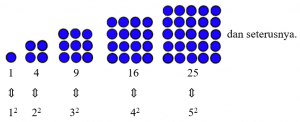
Barisan Bilangan Persegi
Bilangan persegi adalah 1, 4, 9, 16, 25, … .
Contoh :
![]()
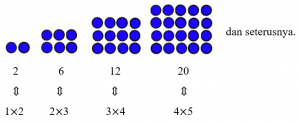
Barisan Bilangan Persegi Panjang
Barisan bilangan persegi panjang adalah 2, 6, 12, 20, … .
Contoh :
![]()
Barisan Bilangan Fibbonacci
Barisan bilangan Fibonacci adalah suatu barisan bilangan yang merupakan hasil penjumlahan dua bilangan sebelumnya.
Contoh :
1, 1, 2, 3, 5, 8, 13, 21, … .
![]()
Barisan Bilangan pada Segitiga Pascal
Contoh :
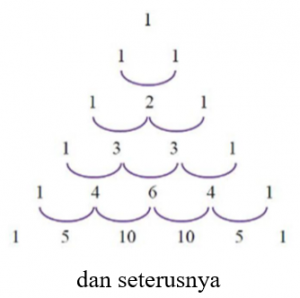
Beberapa sifat dari barisan bilangan pada segitiga pascal yaitu:
- Pada setiap baris diawali dan diakhiri dengan bilangan 1
- Setiap bilangan diperoleh dengan menjumlah dua bilangan di atasnya kecuali bilangan pada baris pertama dan kedua.
- Bilangan dalam satu diagonal membentuk suatu barisan
Diagonal ke-1 : 1, 1, 1, 1, 1, …. (barisan bilangan konstan)
Diagonal ke-2 : 1, 2, 3, 4, 5, …. (barisan bilangan asli)
Diagonal ke-3 : 1, 3, 6, 10, …. (barisan bilangan segitiga)
![]()
Aturan Barisan Bilangan
Beberapa contoh aturan pada barisan bilangan:
Barisan dengan Aturan Ditambah
Barisan Bertingkat Satu
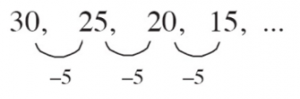
Barisan bilangan 30, 25, 20, 15, … merupakan barisan bertingkat satu.
Biasanya disebut juga sebagai Barisan Aritmetika.
Barisan Bertingkat Dua
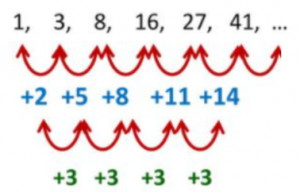
Barisan bilangan 1, 3, 8, 16, 27, 41, … merupakan barisan
bertingkat dua.
![]()
Barisan dengan Aturan Dikali
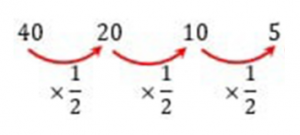
![]()
Barisan dengan Aturan Dipangkatkan

![]()
Rumus Suku Ke-n (Un)

#SEMOGA BERMANFAAT#

Leave A Comment?