Soal nomor 1

Diketahui lima buah bilangan bulat positif yang sudah terurut, yaitu  a + 1, a + 2, 2b – 4, 2b – 2, dan b + 4. Rata-rata lima bilangan tersebut sama dengan jangkauannya dan sama juga dengan mediannya. Nilai (a + b)² adalah….

Pembahasan:

Misalkan:

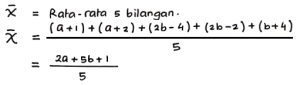
Rata-rata lima bilangan tersebut sama dengan jangkauannya, maka:

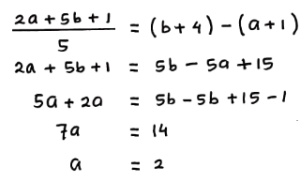
Rata-rata lima bilangan tersebut sama dengan mediannya, maka:

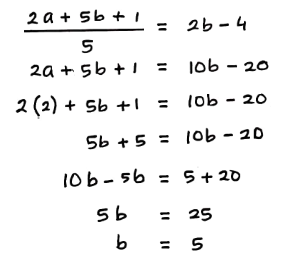
Sehingga, nilai dari:

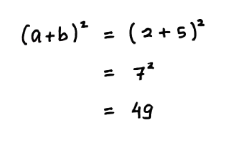
Jadi, nilai dari  (a + b)²  adalah  49.

Soal nomor 2

Sebuah ember berisi 5 bola merah dan 3 bola kuning. Jika seseorang mengambil bola sebanyak 3 kali dan masing-masing dua bola setiap pengambilan tanpa pengembalian. Tentukan peluang bahwa pada setiap pengambilan, bola yang terambil berbeda warna.

Pembahasan:

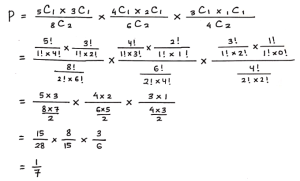
Soal nomor 3

Terdapat 21 bilangan bulat positif pada suatu data, dimana bilangan terbesarnya adalah 16. Median dari data tersebut adalah 10. Hitunglah rata-rata terkecil yang mungkin dari data tersebut.

Pembahasan:

Data untuk rata-rata terkecil:

1, 1, 1, 1, 1, 1, 1, 1, 1, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 16.

Maka Rata-ratanya:

Jadi, rata-rata terkecil yang mungkin dari data tersebut adalah 6.

Soal nomor 4

Diberikan bilangan asli dua digit. Peluang bilangan tersebut memiliki digit penyusun prima dan bersisa 5 jika dibagi 7 adalah….

Pembahasan:

• Bilangan asli dua digit ada 90, yaitu : 10, 11, 12, 13, …, 98, 99.
• Bilangan digit penyusun prima dan bersisa 5 jika dibagi 7 ada 2, yaitu 33 dan 75.

Misalkan:

S     =  bilangan asli dua digit

n(s)  =  90

A      =  bilangan digit penyusun prima dan bersisa 5 jika dibagi 7

n(A)  =  2

Maka peluang A adalah:

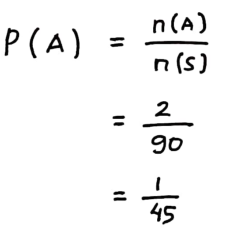
Soal nomor 5

Jika n! = n . (n – 1) . (n – 2) . … . 3 . 2 . 1. Tentukan nilai dari:

1 . 1! + 2 . 2! + 3 . 3! + … + (n – 1) . (n – 1)! + n . n! = ….

Pembahasan:

.

.

.

.

.

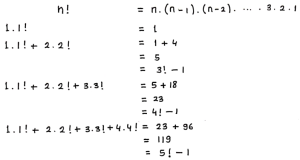
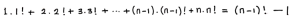
Jadi, nilai dari  1 . 1! + 2 . 2! + 3 . 3! + … + (n – 1) . (n – 1)! + n . n!  =  (n – 1)!  –  1.

Soal nomor 6

Di atas meja terdapat dua set kartu. Setiap set kartu terdiri atas 52 lembar dengan empat warna yang berbeda (merah, kuning, hijau dan biru). Masing-masing warna terdiri atas 13 kartu bernomor 1 sampai 13. Satu kartu akan diambil secara acak dari dua set kartu tersebut. Peluang terambil kartu berwarna merah atau bernomor 13 adalah….

Pembahasan:

Misalkan:

S      =  dua set kartu

n(S)  =  52 × 2  =  104

A      =  kejadian terambil kartu berwarna merah

n(A)  =  13 × 2  =  26

B       =  kejadian terambil kartu bernomor 13

n(B)  =  4 × 2  =  8

Maka:

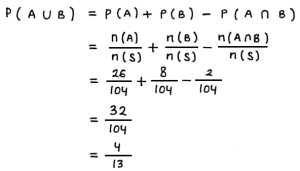
Soal nomor 7

Hitunglah nilai dari:

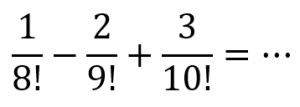
Pembahasan:

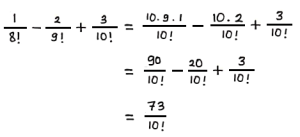
Soal nomor 8

Hasil penjumlahan 1! + 2! + 3! + … + 2022! adalah suatu bilangan yang angka satuannya adalah….

Pembahasan:

1!  =  1

2!  =  2 . 1!  =  1

3!  =  3 . 2!  = 3 . 2  =  6

4!  =  4 . 3!  =  4 . 6  =  24

5!  =  5 . 4!  = 5 . 24  =  120

6!  =  6 . 5!  =  6 . 120  =  ….0

.

.

.

.

2022!  =  2022 . 2021!  =  ….0

Sehingga dapat disimpulkan bahwa:

1! + 2! + 3! + … + 2022!  =  1 + 2 + 6 + 24 + 120 + ….0 + … + ….0  =  ……3

Jadi, hasil penjumlahan 1! + 2! + 3! + … + 2022! adalah suatu bilangan yang angka satuannya adalah 3.

Soal nomor 9

Lima pasangan akan duduk di 10 kursi secara memanjang. Banyak cara mengatur tempat duduk mereka sehingga setiap pasangan tersebut duduk berdampingan adalah….

Pembahasan:

Jadi, banyak cara mengatur tempat duduk mereka sehingga setiap pasangan tersebut duduk berdampingan adalah 3.840 cara.

Soal nomor 10

Sebuah kotak berisi 15 telur, 5 telur diantaranya rusak. Untuk memisahkan telur baik dan telur yang rusak dilakukan pengetesan kepada setiap telur dengan mengambil satu persatu telur tanpa pengembalian. Peluang diperoleh telur rusak ke-3 pada pengetesan ke-5 adalah….

Pembahasan:

Misalkan:

• Pengambilan telur ke-1  =  rusak
• Pengambilan telur ke-2  =  rusak
• Pengambilan telur ke-3  =  baik
• Pengambilan telur ke-4  =  baik
• Pengambilan telur ke-5  =  rusak

Pengambilan ke-5 harus telur yang rusak, maka terdapat 4 tempat tersisa untuk 2 telur yang rusak, sehingga:

Banyak cara pengambilan 2 telur rusak dari 4 tempat yang tersedia adalah:

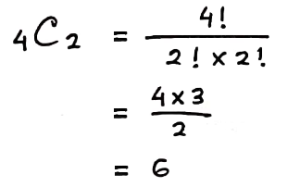
Peluang diperoleh telur rusak ke-3 pada pengetesan ke-5 adalah:

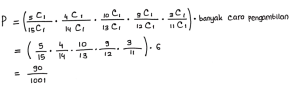
Soal nomor 11

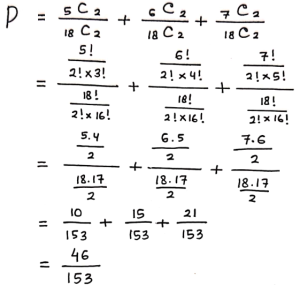
Di dalam kotak terdapat 18 bola yang sama. 5 bola berwarna merah, 6 bola berwarna kuning dan 7 bola berwarna hijau. Jika diambil dua bola secra acak, maka peluang yang terambil bola berwarna sama adalah….

Pembahasan:

Soal nomor 12

Rataan hitung umur kelompok guru dan profesor adalah 40 tahun. Jika rataan hitung kelompok guru adalah 35 tahun sedangkan rataan hitung kelompok profesor adalah 50 tahun, hitunglah perbandingan banyaknya guru dengan profesor.

Pembahasan:

Misalkan:

A  =  umur dari kelompok Guru

B  =  umur dari kelompok Profesor

Maka:

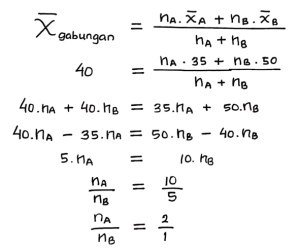
Jadi, perbandingan banyaknya guru dengan profesor adalah 2 : 1.

Soal nomor 13

Lima orang akan pergi ke pantai menggunakan sebuah mobil berkapasitas 6 tempat duduk. Jika hanya ada dua orang yang bisa menjadi sopir, maka banyaknya cara mengatur tempat duduk di dalam mobil adalah….

Pembahasan:

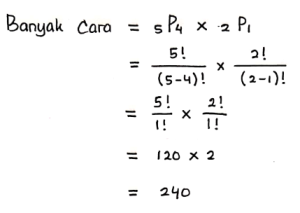
Soal nomor 14

Suatu byte didefinisikan sebagai suusnan angka yang terdiri dari 8 digit angka, yaitu 0 dan 1. Contoh byte: 01001101. Banyak jenis byte yang memuat angka 1 tepat sebanyak 5 adalah….

Pembahasan:

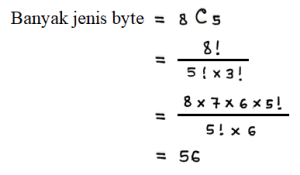
Soal nomor 15

Soal ulangan matematika terdiri atas 5 soal pilihan ganda dengan lima pilihan dan hanya ada satu pilihan yang benar. Jika Rasyil menjawab soal secara menerka (secara acak atau asal-asalan), maka peluang tepat dua soal dijawab dengan benar adalah…

Pembahasan:

#SEMOGA BERMANFAAT#