Soal nomor 1
Di dalam persegi pertama (ABCD) dengan sisi 10 cm, dibangun persegi kedua dengan menghubungkan titik-titik tengah setiap sisi persegi pertama yang bersebelahan. Selanjutnya, dalam persegi kedua dibangun persegi ketiga dengan meghubungkan titik-titik tengah setiap sisi persegi kedua yang bersebelahan. Proses ini berulang sampai menghasilkan lima persegi seperti pada gambar berikut.
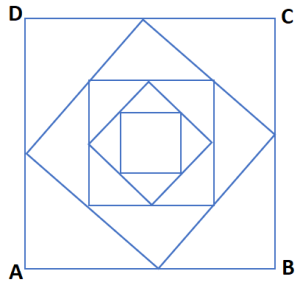
![]()
Tentukan:
- Nilai dari a + b
- Luas persegi besar ketiga
Pembahasan:
Kita buat gambar berikut.
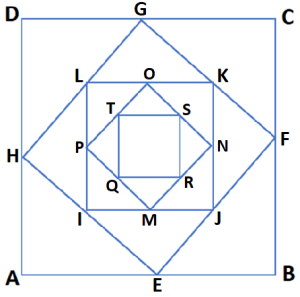
Panjang AB = BC = CD = AD = 10 cm
![]()
Lihat ΔHAE :
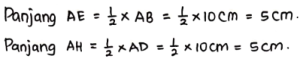
Karena ΔHAE merupakan segitiga siku-siku, sehingga berlaku Teorema Pythagoras:
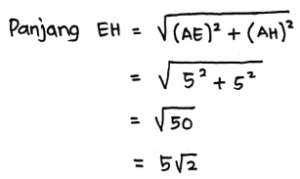
Jadi panjang EH = ![]() cm, sehingga Panjang EH = EF = FG = GH =
cm, sehingga Panjang EH = EF = FG = GH = ![]() cm.
cm.
![]()
Lihat ΔIEJ :
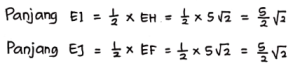
Karena ΔIEJ merupakan segitiga siku-siku, sehingga berlaku Teorema Pythagoras:
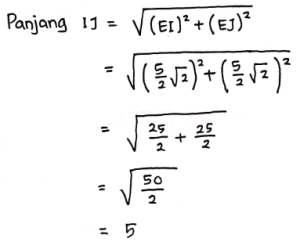
Jadi panjang IJ = 5 cm, sehingga Panjang IJ = JK = KL = IL = 5 cm.
![]()
Lihat ΔPIM :
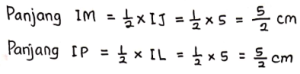
Karena ΔPIM merupakan segitiga siku-siku, sehingga berlaku Teorema Pythagoras:
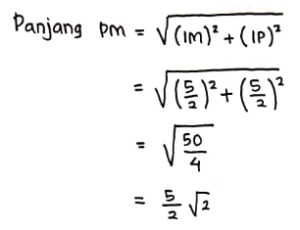
Jadi panjang PM = ![]() cm, sehingga Panjang PM = MN = NO = OP =
cm, sehingga Panjang PM = MN = NO = OP = ![]() cm.
cm.
![]()
Lihat ΔQMR :
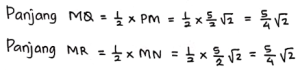
Karena ΔQMR merupakan segitiga siku-siku, sehingga berlaku Teorema Pythagoras:
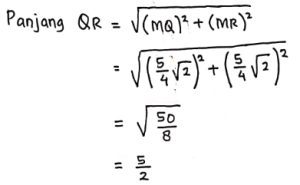
Jadi panjang QR = ![]() cm, sehingga Panjang QR = RS = ST = QT =
cm, sehingga Panjang QR = RS = ST = QT = ![]() cm.
cm.
![]()
- Keliling persegi ABCD = 4 x sisi
= 4 x AB
= 4 x 10 cm
= 40 cm
- Keliling persegi EFGH = 4 x sisi
= 4 x EF
= 4 x ![]()
= ![]() cm
cm
- Keliling persegi IJKL = 4 x sisi
= 4 x IJ
= 4 x 5 cm
= 20 cm
- Keliling persegi MNOP = 4 x sisi
= 4 x MN
= 4 x ![]()
= ![]() cm
cm
- Keliling persegi QRST = 4 x sisi
= 4 x QR
= 4 x ![]() cm
cm
= 10 cm.
![]()
1) Jumlah keliling kelima persegi:
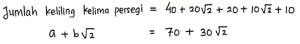
Dari penjelasan di atas, didapat:
Nilai a = 70 cm
Nilai b = 30 cm
Jadi, Nilai a + b = 70 cm + 30 cm = 100 cm.
2) Luas persegi besar ketiga = Luas persegi IJKL
= sisi x sisi
= IJ x KL
= 5 cm x 5 cm
= 25 cm²
Jadi, Luas persegi besar ketiga adalah 25 cm².
![]()
Soal nomor 2
Perhatikan gambar berikut.
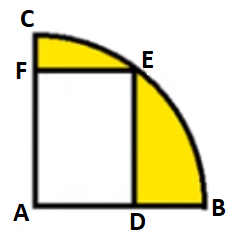
Diketahui panjang AC = 8 cm dan ADFE adalah sebuah persegi panjang dengan keliling 20 cm. Jika luas daerah yang berwarna kuning adalah (aπ + b) cm².
Tentukan :
- Nilai dari a – b
- Keliling daerah yang berwarna kuning
Pembahasan:
Lihat persegi panjang ADEF
Keliling persegi panjang ADEF = 2 (panjang + lebar)
20 cm = 2 (DE + AD)
DE + AD = 10 cm.
![]()
Panjang AB = AC = AE = 8 cm (Panjang Jari-jari)
![]()
Lihat ΔADE:
Segitiga ADE merupakan segitiga siku-siku, sehingga berlaku Teorema Pythagoras:
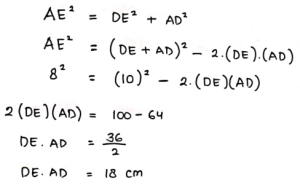
![]()
Perhatikan seperempat lingkaran ABC
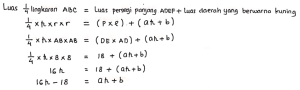
1. Dari penjelasan di atas, didapat:
Nilai a = 16 cm
Nilai b = -18 cm
Jadi, Nilai a – b = 16 cm – (-18 cm) = 34 cm.
![]()
2. Keliling daerah yang berwarna kuning
Catatan: panjang AD = EF dan panjang DE = AF
Keliling daerah = BC + CF + EF + DE + BD
= (Seperempat x Keliling Lingkaran) + (CF + DE) + (EF + BD)
= (![]() ) + AC + AB
) + AC + AB
= (![]() ) + 8 + 8
) + 8 + 8
= ![]() + 16
+ 16
Jadi, keliling daerah yang berwarna kuning = 4π + 16.
![]()

Leave A Comment?