Soal nomor 1
Diketahui a, b, c, dan d adalah bilangan bulat positif berbeda yang merupakan faktor dari 2.022 dan faktor persekutuan terbesar (FPB) setiap bilangan a, b, c, dan d adalah 1. Jika:
d = b(4c + a)² – a dan nilai dari a + b + c + d = e³, maka tentukan nilai e.
Pembahasan:
2.022 = 2 x 3 x 337
faktor persekutuan terbesar (FPB) setiap bilangan a, b, c, dan d adalah 1, sehingga:
2.022 = 1 x 2 x 3 x 337 ![]() (a x b x c x d)
(a x b x c x d)
![]()
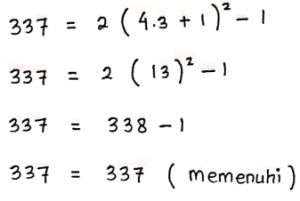
Sehingga, didapat Nilai:
a = 1
b = 2
c = 3
d = 337
Maka, nilai dari:
a + b + c + d = e³
1 + 2 + 3 + 337 = e³
343 = e³
e = ![]()
e = 7
Jadi, Nilai dari e adalah 7.
![]()
Soal nomor 2
Jika diketahui (a + b) = 5, (b + c) = 6, dan (c + a) = 7, maka nilai a + b + c = …
Pembahasan:
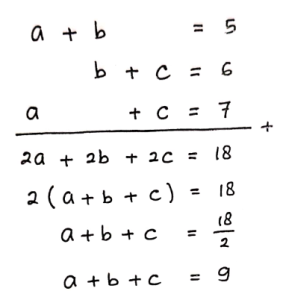
Jadi, nilai a + b + c = = 9.
![]()
Soal nomor 3
Diketahui bilangan bulat positif a sehingga
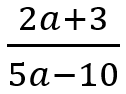
merupakan bilangan bulat positif. Dua nilai a yang memenuhi adalah….
Pembahasan:
Misalkan:
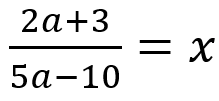
Sehingga:
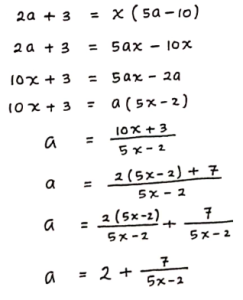
Agar nilai a bernilai bilangan bulat positif, maka penyebut (5x – 2) juga harus bernilai bilangan bulat positif. Maka dari itu, pembagi dari (5x – 2) harus merupakan faktor dari pembilangnya, yaitu 7 (Faktor dari 7 adalah 1 dan 7), Sehingga:
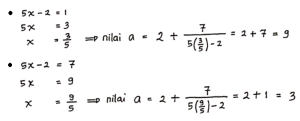
Jadi, Nilai a yang memenuhi adalah a = 3 dan a = 9.
![]()
Soal nomor 4
Misalkan a, b, dan c adalah bilangan real positif yang memenuhi system persamaan berikut.
a + b + c = 6
a² + b² + c² = 20
a³ + b³ + c³ = 72
Tentukan nilai dari:
![]()
Pembahasan:
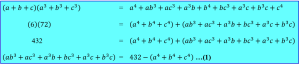
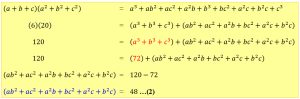
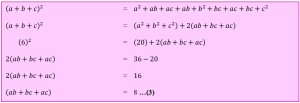

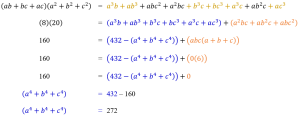

Leave A Comment?