Lihat Materi: Integral

Soal nomor 1

Tentukan hasil dari integral berikut:

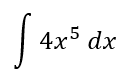
Pembahasan:

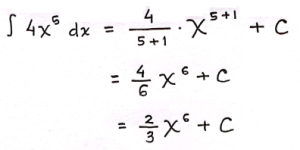
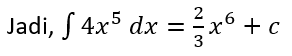
Soal nomor 2

Tentukan hasil dari integral berikut:

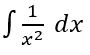
Pembahasan:

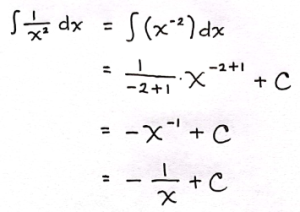
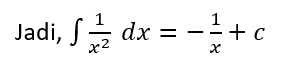
Soal nomor 3

Tentukan hasil dari integral berikut:

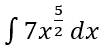
Pembahasan:

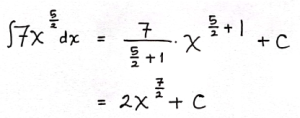
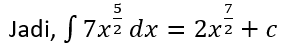
Soal nomor 4

Tentukan hasil dari integral berikut:

Pembahasan:

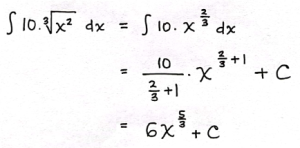
Soal nomor 5

Tentukan hasil dari integral berikut:

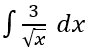
Pembahasan:

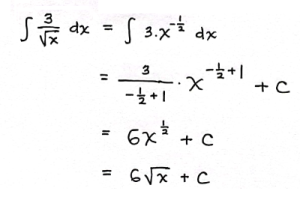
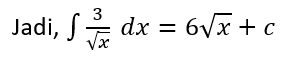
Soal nomor 6

Tentukan hasil dari integral berikut:

Pembahasan:

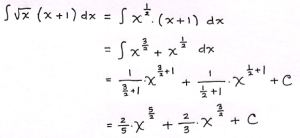
Soal nomor 7

Tentukan hasil dari integral berikut:

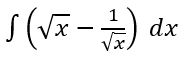
Pembahasan:

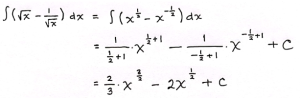
Soal nomor 8

Tentukan hasil dari integral berikut:

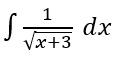
Pembahasan:

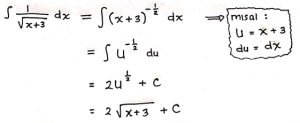
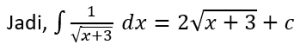
Soal nomor 9

Tentukan hasil dari integral berikut:

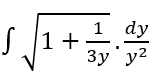
Pembahasan:

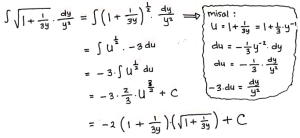
Soal nomor 10

Tentukan hasil dari integral berikut:

Pembahasan:

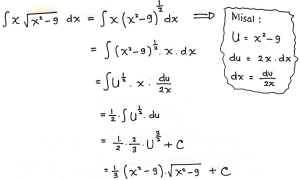
Soal nomor 11

Diketahui turunan fungsi  f  dinyatakan dengan  f’(x) = 6x² – 3x + 4, dan nilai fungsi f(3) = 72. Tentukan rumus fungsi tersebut.

Pembahasan:

f(x)  =  ∫ f’(x) dx

f(x)  =  ∫ (6x² – 2x + 4) dx

f(x)  = 2x³ – x² + 4x + C

Karena f(3) = 12, maka:

f(x)  = 2x³ – x² + 4x + C

f(3)  = 2(3)³ – (3)² + 4(3) + C

72   =  57 + C

C     =  15

Jadi, f(x)  = 2x³ – x² + 4x + 15

Soal nomor 12

Hitunglah integral tak tentu berikut.

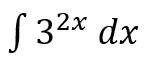
Pembahasan:

Misalkan :

U = 2x

du = 2 dx

Sehingga:

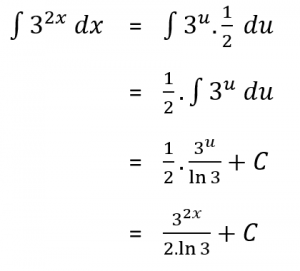
Jadi,

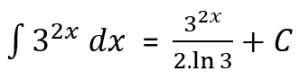
Soal nomor 13

Hitunglah integral tak tentu berikut.

Pembahasan:

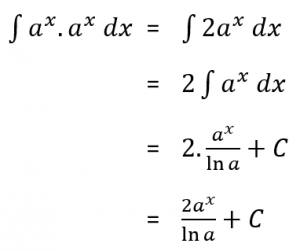
Jadi,

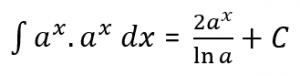
Soal nomor 14

Hitunglah integral tak tentu berikut.

Pembahasan:

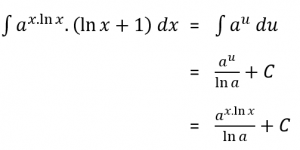
Jadi,

Soal nomor 15

Hitunglah integral tak tentu berikut.

Pembahasan:

Misalkan:

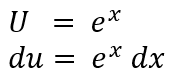
Sehingga:

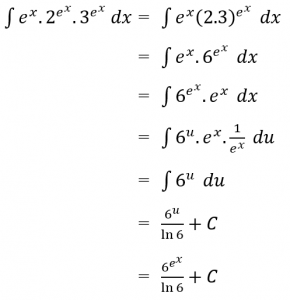
Jadi,

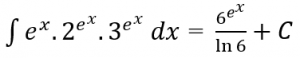
Soal nomor 16

Hitunglah integral tak tentu berikut.

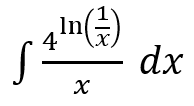
Pembahasan:

Misalkan:

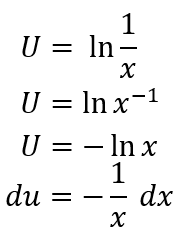
Sehingga:

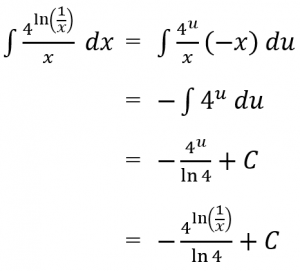
Jadi,

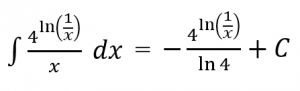
Soal nomor 17

Hitunglah integral tak tentu berikut.

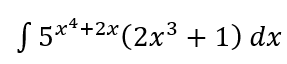
Pembahasan:

Misalkan:

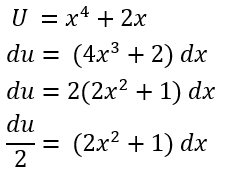
Sehingga:

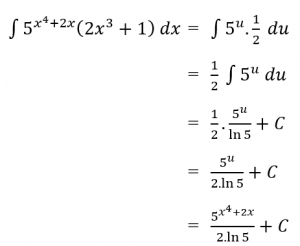
Jadi,

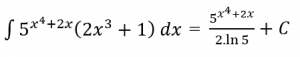
Soal nomor 18

Hitunglah integral tak tentu berikut.

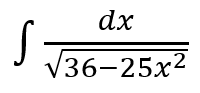
Pembahasan:

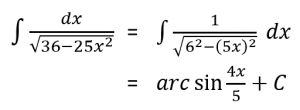
Jadi,

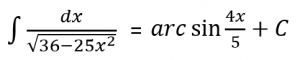
Soal nomor 19

Hitunglah integral tak tentu berikut.

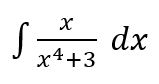
Pembahasan:

Misalkan:

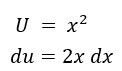
Sehingga:

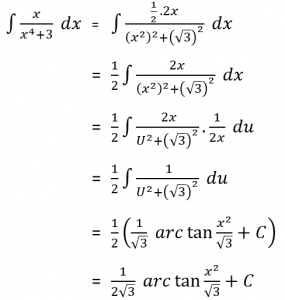
Jadi,

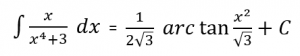
Soal nomor 20

Hitunglah integral tak tentu berikut.

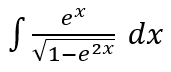
Pembahasan:

Misalkan:

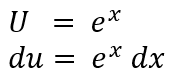
Sehingga:

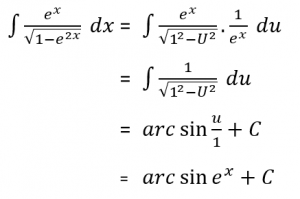
Jadi,

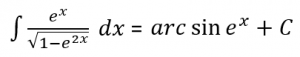
Soal nomor 21

Hitunglah integral tak tentu berikut.

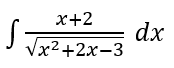
Pembahasan:

Misalkan:

U  = x² + 2x – 3

du = 2x + 2

Sehingga:

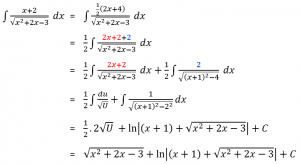
Jadi,

Soal nomor 22

Hitunglah integral tak tentu berikut.

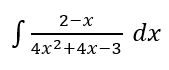
Pembahasan:

Misalkan:

U = (2x + 1)

du = 2 dx

Sehingga:

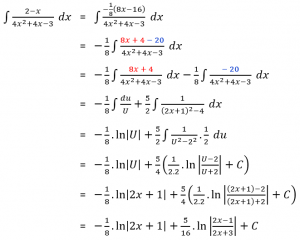
Jadi,

Soal nomor 23

Hitunglah integral tak tentu berikut.

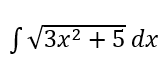
Pembahasan:

Misalkan:

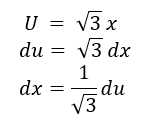
Sehingga:

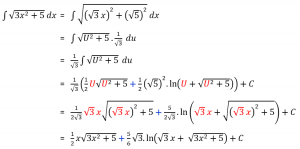
Jadi,

#SEMOGA BERMANFAAT#