Soal nomor 1

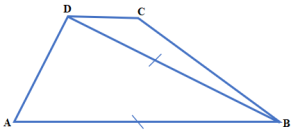
Diketahui trapesium ABCD, dengan AB // CD. Jika diagonal BD dan sisi AB sama panjang dan ∠BCD = 115° serta ∠CBD = 25°. Tentukan jumlah dari  ∠BDC dan ∠ADB.

Pembahasan:

Baca Materi : Sudut Dalam Segitiga

• Lihat ΔBCD

Jumlah sudut dalam suatu segitiga  =  180°

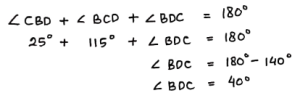
Karena  AB // CD, maka ∠BDC = ∠ABD = 40°.

• Lihat ΔABD

Karena panjang BD = AB, maka ∠BAD = ∠ADB

Jumlah sudut dalam suatu segitiga   =  180°

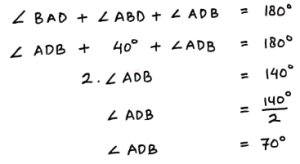
Jadi, jumlah dari  ∠BDC dan ∠ADB  =  40° + 70°  =  110°.

Soal nomor 2

Perhatikan gambar berikut.

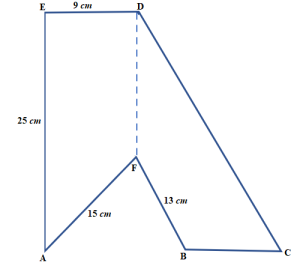
Diketahui A, B, C segaris dan Garis ED // BC. Luas daerah AFBCDE adalah 416 cm². Hitunglah :

a. Luas segitiga ABF

b. Panjang BC

Pembahasan:

Kita bahas ya…

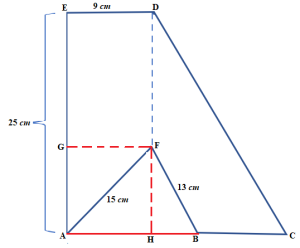
Diketahui :

Luas daerah AFBCDE = 416 cm²

Panjang DE = FG = AH = 9 cm

Panjang AF = 15 cm

Panjang BF = 13 cm

Panjang AE = 25 cm

Lihat ΔAFG

Segitiga AFG merupakan segitiga siku-siku, sehingga berlaku Teorema Pythagoras:

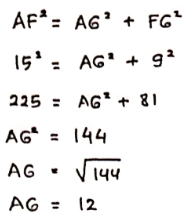
Sehingga Panjang AG = FH = 12 cm

Lihat ΔBHF

Segitiga BHF merupakan segitiga siku-siku, sehingga berlaku Teorema Pythagoras:

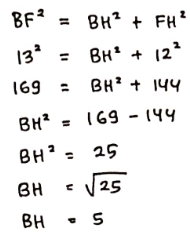
a. Luas segitiga ABF

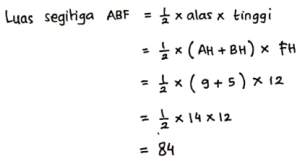
Jadi, Luas segitiga ABF = 84 cm².

b. Panjang BC

Jadi, Panjang BC = 17 cm.

#SEMOGA BERMANFAAT#